Question

A go cart starts from rest and accelerates to 30m/s^2 in a distance of 75m. If the force ofthe engine is 600N and the frictional force is 120N, find the mass of the cart.

Answer 1

Given:

• Acceleration, a = 30 m/s²

,

• Distance, d = 74 m

,

• Force, F = 600 N

,

• Frictional force, Ff = 120 N

Let's find the mass of the cart.

To find the mass of the cart, apply Newton's Second Law:

`F_(net)=m*a`

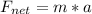
Where:

Fnet is the net force

m is the mass

a is the acceleration.

To find the net force, we have:

`\begin{gathered} F_(net)=F-F_f \\ \end{gathered}`

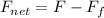
Thus, we have:

`\begin{gathered} F-F_f=m*a \\ \\ 600-120=m*30 \\ \\ m=(600-120)/(30) \\ \\ m=(480)/(30) \\ \end{gathered}`

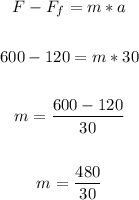
Solving further:

`m=16\text{ kg}`

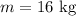
Therefore, the mass of the cart is 16 kg.

• ANSWER:

16 kg