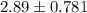Question

Find the MEAN MAD VARIANCE AND STANDARD DEVIATION round to the nearest cent

Answer 1

Let's start putting all the data on the paper. 6 different jars of pasta sauce with the prices

{$2.79, $1.99,$ 4.29,$2.49,$2.29,$3.49}. To find the mean you have to sum all these values and then divide them by the number of jars (total is 6). So:

`\text{Mean = }(2.79+1.99+4.29+2.49+2.29+3.49)/(6)=2.89`

To calculate the MAD value you should first calculate the mean (It's $2.89 that we have calculated). Then we have to calculate the 'distance' between each data and the mean (these are the first two steps). So let's start doing:

`Each\text{ value - mean}`
`\mathrm{abs}(2.79-2.89)\text{ = 0.1}`
`\mathrm{abs}(1.99-2.89)\text{ = 0}.9`
`\mathrm{abs}(4.29-2.89)\text{ = }1,4`
`\mathrm{abs}(2,49-2.89)\text{ = 0}.4`
`\mathrm{abs}(2.29-2.89)\text{ = 0}.6`
`\mathrm{abs}(3.49-2.89)\text{ = 0}.6`

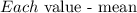
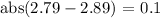
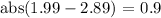
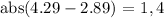
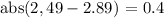
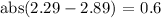
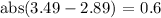
Now we have to sum all these distances:

`0.1+0.9+1.4+0.4+0.6+0.6=4`

MAD (Median Absolute Deviation) gives a measure of the variability of the data! You can calculate the value dividing the sum of the distances by the number of total jars:

`\text{MAD = }(4)/(6)=0.67`

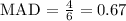
The next item is to calculate the Variance. The formula of variance is:

`\text{Var = }\frac{(Data-Mean)^2\ldots.}{\text{Total}}`

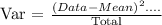
So we have to get each value and subtract by the mean everything squared. Is another way to measure the dispersion.

`\text{Var = }\frac{(2.79-2.89)^2+(1.99-2.89^{})^2+(4.29-2.89)^2+(2.49-2.89)^2+(2.29-2.89)^2+(3.49-2.89)^2^{}^{}^{}}{6}`
`\text{Var =0.61}`

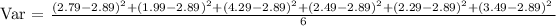
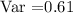
Finally, we can find the Standart Deviation. The standard deviation can be found using the square root of the Variance. Standard Deviation is a measure of how trustable the mean is.

`\text{Standart = }\sqrt[]{Variance}`
`\text{Stantard = }\sqrt[]{0.61}=0.781`

Example of the use of the Standart Deviation

If we talk that the mean is 2.89 we have to consider the deviation (information about the data reliability):

`2.89\pm0.781`