Question

On a particular college campus, 22% of the students belong to a fraternity or sorority. If 56 college students are randomly chosen:a. What is the probability that no more than 16 are members of a fraternity or sorority?Round to at least three decimal places.b. What is the mean of this distribution? Round to at least one decimal.c. What is the standard deviation of this distribution? Round to at least one decimal.

Answer 1

Given:

`\begin{gathered} p_o=22\text{ \%}=(22)/(100) \\ p_o=0.22 \\ n=56 \end{gathered}`
`\hat{p}=(16)/(56)=0.286`

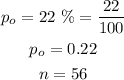
Using the Z-score formula below;

`\begin{gathered} Z=\frac{\hat{p}-p_o}{\sqrt{(p_o(1-p_o))/(n)}} \\ \\ Substituting\text{ the given and calculated values;} \\ Z=\frac{0.286-0.22}{\sqrt{(0.22(1-0.22))/(56)}} \\ Z=\frac{0.066}{\sqrt{(0.22*0.78)/(56)}} \\ Z=(0.066)/(√(0.003064)) \\ Z=1.192 \end{gathered}`

Question a:

The probability that no more than 16 are members of a fraternity or sorority is;

`\begin{gathered} From\text{ Z-score tables,} \\ P(Z\leq1.192)=0.8834 \\ \\ To\text{ three decimal places,} \\ P(Z\leq1.192)=0.883 \end{gathered}`

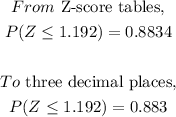
Therefore, to three decimal places, the probability that no more than 16 are members of a fraternity or sorority is 0.883

Question b:

The mean of the distribution is;

`\begin{gathered} mean=np_o \\ mean=56*0.22 \\ mean=12.32 \\ \\ To\text{ one decimal place,} \\ mean=12.3 \end{gathered}`

Therefore, to one decimal place, the mean of the distribution is 12.3

Question c:

The standard deviation of the distribution is;

`\begin{gathered} \sigma=√(npq) \\ where: \\ q=1-p \\ q=1-0.22=0.78 \\ \sigma=√(56*0.22*0.78) \\ \sigma=√(9.6096) \\ \sigma=3.0999 \\ \\ To\text{ one decimal place;} \\ \sigma=3.1 \end{gathered}`

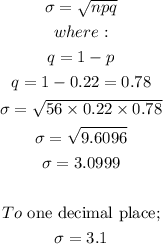
Therefore, to one decimal place, the standard deviation of the distribution is 3.1