1 Answer

Belder · Answer 1 · 2023-03-30T09:58:57+0000

For the given quadrilateral to be a parallelogram, opposite sides must be congruent.

Therefore,

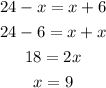
$\begin{gathered} 24-x=x+6 \\ 24-6=x+x \\ 18=2x \\ x=9 \end{gathered}$
x+6=9+6=15

Also, we have that:

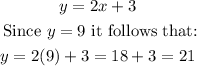
$\begin{gathered} y=2x+3 \\ \text{ Since }y=9\text{ it follows that:} \\ y=2(9)+3=18+3=21 \end{gathered}$

Therefore, y = 21 and x = 9

Hence, the perimeter is given by:

$2(15+21)=72\text{ units}$

Therefore, the values of x and y are y = 21 and x = 9.

The perimeter is 72 units

Please log in or register to add a comment.