Answer:
• The amount put in the bank = $1,500
• The amount used to buy bond = $500
,
• The amount used to buy the certificate of deposit =$8000
Step-by-step explanation:
Bank (5%)
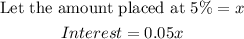
Bonds (6%)
1/3 the amount placed in the bank was used to buy bonds

Certificate of Deposit (8%)
If the total of the investments is $10,000, the balance of the funds will be:
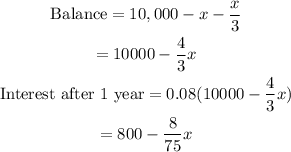
![undefined]()
The first year, the investments bring a return of $745. Therefore, we sum up all the interests:
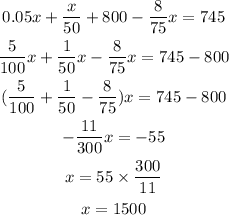
Thus:
• The amount put in the bank = $1,500
,
• The amount used to buy bond = 1500/3 = $500
,
• The amount used to buy certificate of deposit = 10,000-2000=$8000