Given:

The formula for general term is:
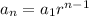
Thus, we can write:
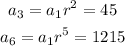
We can divide a_6 by a_3:
![\begin{gathered} (a_6)/(a_3) \\ (a_1r^5)/(a_1r^2)=(1215)/(45) \\ (r^5)/(r^2)=27 \\ r^(5-2)=27 \\ r^3=27 \\ r=\sqrt[3]{27} \\ r=3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vtdzz26m87znijj1w2scp700x4qzwds1ef.png)
We found r = 3.
Now, we need first term, a_1.
So,

So,
First Term = 5
Common Ratio = 3
The general term of this geometric sequence is:
So,
First Term = 5
Common Ratio = 3
The general term of this geometric sequence is: