Question

3x + 2y = 12 at x-intercept: b. y-intercept: c. graph 10+ 9 8 7 6 13 17 2 -10-9-8-7 -6 -5 7 -3 -2 -1, B 4 55 6 8 g 10 -5 -6 -7 -8 -9 10 Clear All Draw:

Answer 1

`3x+2y=12`

a. x- intercept: the point at which the graph crosses the x-axis, when the y-value is 0.

To find the x- intercept in the given equation substitute the y by 0 and solve for x:

`\begin{gathered} 3x+2(0)=12 \\ 3x+0=12 \\ 3x=12 \\ \\ \text{Divide both sides of the equation into 3:} \\ (3)/(3)x=(12)/(3) \\ \\ x=4 \end{gathered}`

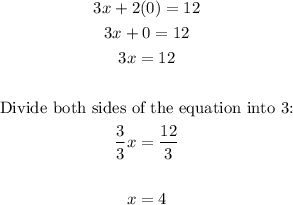
Then, the x-intercept is ( 4, 0 )

b. y-intercept: the point at which the graph crosses the y-axis, when the x-value is 0.

To find the y-intercept in the givne equation substitute the x by 0 and solve for x:

`\begin{gathered} 3(0)+2y=12 \\ 0+2y=12 \\ 2y=12 \\ \\ \text{Divide both sides of the equation into 2:} \\ (2)/(2)y=(12)/(2) \\ \\ y=6 \end{gathered}`

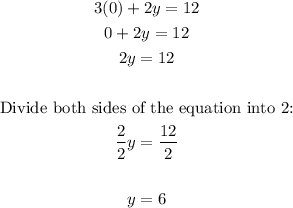
Then, the y-intercept is ( 0 , 6 )

c. Graph: Use the x-intercept and y-intercept, put it in the plane and then draw a line that passes trough those points: