The information given can be represented in the diagram below
From the rhombus above, E is the perpendicular bisector of the diagonals AC and BD.
Let BD = 32cm, AC = 60cm (given)
Using Pythagoras theorem,
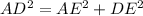
![\begin{gathered} AE=(1)/(2)* AC \\ AE=(1)/(2)*60\operatorname{cm} \\ AE=30\operatorname{cm} \end{gathered}]()
![\begin{gathered} DE=(1)/(2)* BD \\ DE=(1)/(2)*32\operatorname{cm} \\ DE=16\operatorname{cm} \end{gathered}]()
Using Pythagoras theorem
![\begin{gathered} AD^2=AE^2+DE^2 \\ AD^2=30^2+16^2 \\ AD^2=900+256 \\ AD^2=1156 \\ AD=\sqrt[]{1156} \\ AD=34\operatorname{cm} \end{gathered}]()
The perimeter of the rhombus would be
![\begin{gathered} P_{\rho\text{mbus}}=AB+BC+CD+AD \\ \text{Note,} \\ AB=BC=CD=AD=34\operatorname{cm} \\ P_{\rho\text{mbus}}=4AD \\ P_{\rho\text{mbus}}=4*34 \\ P_{\rho\text{mbus}}=136\operatorname{cm} \end{gathered}]()
Hence, the perimeter of the given rhombus is 136cm