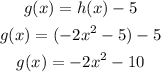Question

The function h is defined as follows. h(x) = - 2x ^ 2 - 5 If the graph of h is translated vertically downward by 5 units, it becomes the graph of a function g, Find the expression for g(x)

Answer 1

The answer is :

`g(x)=-2x^2-10`

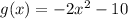
EXPLANATION :

From the problem, we have :

`h(x)=-2x^2-5`

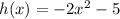
h(x) is translated vertically by 5 units downward and it becomes the graph of a function g.

So g(x) = h(x) - 5

negative 5 denotes that h(x) is translated 5 units downward.

So that will be :

`\begin{gathered} g(x)=h(x)-5 \\ g(x)=(-2x^2-5)-5 \\ g(x)=-2x^2-10 \end{gathered}`