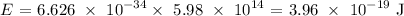Question

Green light has the wavelength of 5.0x 10^2 nm. what is the energy, in joules, of one photon of green light?

Answer 1

`3.96\text{ }*\text{ 10}^(-19)\text{ J}`

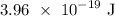
Step-by-step explanation:

Here, we want to get the energy in Joules

Given:

`\begin{gathered} wavelength\text{ \lparen}\lambda)\text{ = 5.02 }*\text{ 10}^2\text{ nm} \\ 1\text{ nm = 1}*\text{ 10}^(-9)\text{ m} \\ wavelength\text{ = 5.02 }*\text{ 10}^(-7)\text{ m} \end{gathered}`

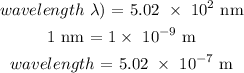
The frequency of light can be calculated using the formula as follows:

`\begin{gathered} f\text{= }(c)/(\lambda) \\ \\ c\text{ = speed of light = 3 }*\text{ 10}^8\text{ ms}^(-1) \end{gathered}`

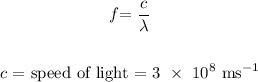
Calculating the frequency, we have it that:

`\text{ f = }(3*10^8)/(5.02*10^(-7))\text{ = 5.98 }*\text{ 10}^(14)\text{ S}^(-1)`

The Energy of a photon is calculated as:

`\begin{gathered} E\text{ = hf} \\ h\text{ = Planck's constant = 6.626 }*\text{ 10}^(-34)\text{ Js} \end{gathered}`

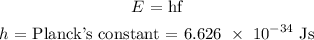
We proceed to multiply this with the frequency above as follows:

`E\text{ = 6.626 }*\text{ 10}^(-34)*\text{ 5.98 }*\text{ 10}^(14)\text{ = 3.96 }*\text{ 10}^(-19)\text{ J}`