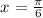ANSWER:
General solution:
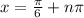
Solution over the given interval:
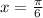
Step-by-step explanation:
Let's solve for tan(x),
![\begin{gathered} 2\sqrt[]{3}\tan (x)-2=0\rightarrow2\sqrt[]{3}\tan (x)=2 \\ \rightarrow\sqrt[]{3}\tan (x)=1\rightarrow\tan (x)=\frac{1}{\sqrt[]{3}} \\ \\ \Rightarrow\tan (x)=\frac{\sqrt[]{3}}{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/j9xz2p994e6iwr2870gv1s9pb9gtyg5qy7.png)
Now, we'll use the inverse trigonometric function for tangent:
![\begin{gathered} \tan (x)=\frac{\sqrt[]{3}}{3}\rightarrow x=\tan ^(-1)(\frac{\sqrt[]{3}}{3}) \\ \\ \Rightarrow x=(\pi)/(6) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/iz5b5nz7ye78kad3x7i40x389g9o38i5u4.png)
Now, since tan(x) has a period of pi, the general solution for the equation is:
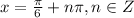
For the interval [0,pi] we'll have the solution: