We have a rectangle that has a width that is 2 inches longer than its height.
We know that the diagonal is 28 inches long.
We can draw this as:
We can use the Pythagorean theorem to relate the measures as:
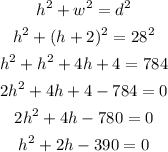
The height will come from the solution of this quadratic equation:
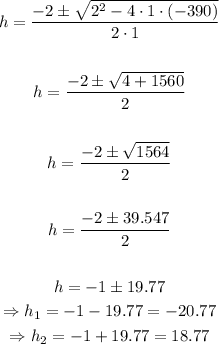
The negative solution does not make sense in the context of the problem, so the solution to this problem is h = 18.8 inches.
Answer: the height is approximately 18.8 inches.