Question

How do I write an equation to describe this graph?

Answer 1

From the given picture, we can to note that the major axis is located on the x-axis. So, the ellipse equation has the form

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

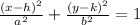
where (h,k) is the coordinate of the center, a is the distance from the center one vertex (the one located on the major axis) and b is the distance from the center to the minor axis vertex, that is,

Then, from the picture above, we can note that

`\begin{gathered} a=6 \\ b=4 \\ (h,k)=(0,0) \end{gathered}`

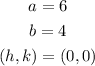
So, by substituting these values into our first equation, we get

`((x-0)^2)/(6^2)+((y-0)^2)/(4^2)=1`

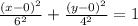
Therefore, the answer the ellipse equation is:

`(x^2)/(36)+(y^2)/(16)=1`