Question

When Ryan runs on the treadmill at the gym, the number of calories,c, he burns varies directly with the number of minutes,m, he uses the treadmill. He burned 315 calories when he used the treadmill for 18 minutes.a)write the equation that relates c and m.b)how many calories would he burn if he ran on the treadmill for 25 minutes?

Answer 1

A linear equation or a function that varies directly is represented by the following expression:

`\begin{gathered} y=kx \\ \text{where, k is the constant rate of change } \end{gathered}`

To determine the constant rate of change between the variables, let's substitute y=315 calories, x=18 minutes

`\begin{gathered} 315=18k \\ k=(315)/(18) \\ k=17.5 \end{gathered}`

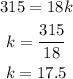
Therefore, an equation that represents the situation would be

Let c be the number of calories he burns

Let m be the number of minutes he uses the treadmill

`c=17.5m`

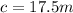
To determine how many calories would he burn in 25 minutes, we must substitute m=25

`\begin{gathered} c=17.5\cdot25 \\ c=437.5 \end{gathered}`

After 25 minutes he would burn 437.5 calories