We know that f(x) is a linear function.
We also know two points of the function:
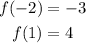
We can calculate the slope of f(x) as:
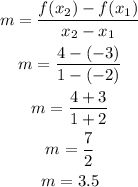
With the slope m = 3.5 and one point, like (1, 4), we can write the equation in slope-point form and then rearrange:
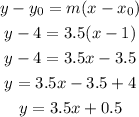
Answer: the equation is f(x) = 3.5x + 0.5