Given:
The count of bacteria was 100 after 15 minutes and 1300 after 30 minutes.
To find:
1. The initial size of the culture.
2. The doubling period.
3. Find the population after 115 minutes.
4. The time at which population 15000.
Solution:
The growth is exponential. Let the equation that shows the bacteria after t minutes is given by:

It is given that The count of bacteria was 100 after 15 minutes and 1300 after 30 minutes. So,
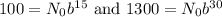
Divide first equation by second to get:
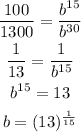
Put b = 1.186 in the first equation and solve for N_0:
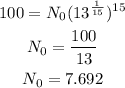
Thus, the initial size of the culture is 7.692.
To find doubling time, find the time taken to reach 200 count.
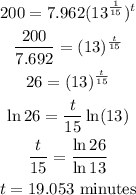
So, the time taken to double the count is 19.053 - 15 = 4.053 minutes.
The population after 115 minutes is given by:
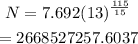
Thus, the population after 115 minutes is 2668527257.6037.
The time taken to reach the population 15000 can be obtained as follows:
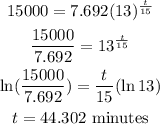
Thus, the population reaches 15000 after 44.302 minutes.