To solve the equation, we can do the following steps:
![\begin{gathered} \sqrt[]{x}+2=x \\ \text{ Subtract 2 from both sides of the equation} \\ \sqrt[]{x}+2-2=x-2 \\ \sqrt[]{x}=x-2 \\ \text{Raise both sides of the equation to the power 2} \\ (\sqrt[]{x})^2=(x-2)^2 \\ x=(x-2)^2 \\ x=(x-2)(x-2) \\ \text{ Apply the distributive property} \\ x=(x-2)(x-2) \\ x=x\cdot x-2\cdot x-2\cdot x+2\cdot2 \\ x=x^2-2x-2x+4 \\ \text{ Subtract x from both sides of the equation} \\ x-x=x^2-2x-2x+4-x \\ \text{ Add similar terms} \\ 0=x^2-5x+4 \\ \text{ Factor} \\ 0=(x-4)(x-1) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/b5wb9hzdpbrudn1d0orcse7k9jgc154n39.png)
Then, there are two possible solutions:
• First one:
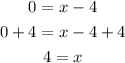
• Second one:
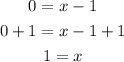
Now, we verify which of the solutions found satisfies the original equation:
• First one:
![\begin{gathered} x=4 \\ \sqrt[]{x}+2=x \\ \sqrt[]{4}+2=4 \\ 2+2=4 \\ \text{ True} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/a64f3sxx6aujc8otkr4ecjopmcmb2efqyg.png)
• Second one:
![\begin{gathered} x=1 \\ \sqrt[]{x}+2=x \\ \sqrt[]{1}+2=1 \\ 1+2=1 \\ 3=1 \\ \text{ False} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/liwqkm37mwmn516faozrpsas6lrn37p9ea.png)
Therefore, the solution of the given equation is 4.