Question

Solve your answers using inequalities using a number line strategy or a factor table strategy. Express your answers using set notation. a) (x+4)(x+2)(x-3) ≤ 0b) (x+3)^2 (x+1)(x-1) > 0c) (x+1)(x+3) ≥ 0

Answer 1

Given the inequalitiy;

`(x+4)(x+2)(x-3)\le0`

We begin by finding the factors of this inequality and the appropriate signs, as follows;

`\begin{gathered} x+4=0 \\ x=-4 \\ \text{Also,} \\ x+4<0 \\ x<-4 \\ x+4>0 \\ x>-4 \end{gathered}`

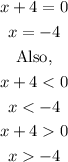
Next we find the signs of x + 2

`\begin{gathered} x+2=0\Rightarrow x=-2 \\ x+2<0\Rightarrow x<-2 \\ x+2>0\Rightarrow x>-2 \end{gathered}`

And now we find the signs of x - 3

`\begin{gathered} x-3=0\Rightarrow x=3 \\ x-3<0\Rightarrow x<3 \\ x-3>0\Rightarrow x>3 \end{gathered}`

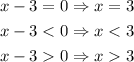
Next step we identify the intervals that satisfy the required condition "less than or equal to zero."

That is;