Question

(1 point) Fawns between 1 and 5 months old in Mesa Verde National Park have a body weight that is approximately normallydistributed with mean I= 25.5 kg and standard deviation o- 4.29 kg. Let 2 be the weight of a fawn in kg. What is theprobability that for a fawn chosen at random:

Answer 1

Explanation

Given: Normally distribution with the following information

`\begin{gathered} \mu=25.5kg \\ \sigma=4.29kg \end{gathered}`

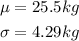
Required: To determine the probability that for a fawn chosen at random:

• x is less than 30.04kg

,

• x is greater than 15.82kg

,

• x is between 31.44 and 33.91kg

This is achieved thus:

First, we can approximate to a standard normal distribution with the formula below:

`Z=(x-\mu)/(\sigma)`

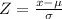
For Part A: x is less than 30.04kg

`\begin{gathered} P(x<30.04)=P(Z<(30.04-25.5)/(4.29)) \\ \Rightarrow P(Z<1.0583) \\ =0.8550 \end{gathered}`

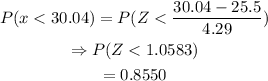
For Part B: x is greater than 15.82kg

`\begin{gathered} P(x>15.82)=P(Z>(15.82-25.5)/(4.29)) \\ \Rightarrow P(Z>-2.2564) \\ =0.9880 \end{gathered}`

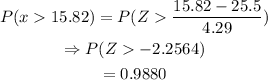
For Part C: x is between 31.44 and 33.91kg