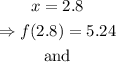To obtain the slope of the tangent line to f(x) at x=2, we need to find f'(x) as shown below
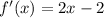
Then, the slope of the tangent line we are looking for is
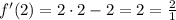
Remember that the slope of a line can be interpreted as shown below
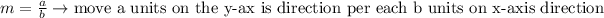
Therefore, we can estimate the value of f(x) using the slope and f(2).
a) x=2.4
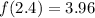
And the estimation using f(2) and f'(2) is

Then, the exact value at x=2.4 is f(2.4)=3.96, and the approximated value is 3.8
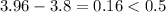
We need to repeat these steps with the remaining options.
b) x=2.5
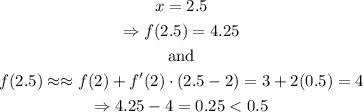
c) x=2.6

d) x=2.7
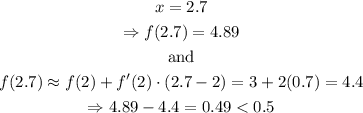
Then, the answer is option d. x=2.7
e) x=2.8