Question

Rachel has a large pond on her property. The pond contains many different kinds of fish including bass. She knows that the population of the bass is increasing exponentially each year at a rate of 4.8%. She also knows that there are currently between 250 and 275 bass in the pond.If P represents the actual population of the bass in the pond and t represents the elapsed time in years, then which of the following systems of inequalities can be used to determine the possible number of bass in the pond over time?

Answer 1

Step-by-step explanation:

Given:

Growth rate=4.8% = 0.048

Initial Amount 1 = 250

Initial Amount

We use the continuous-growth formula below as a guide:

`A=Pe^(rt)`

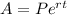
Where:

A= ending amount

P= beginning amount

r= growth rate

t= time

Based on the given problem, we have two initial amounts: 250 and 275. It means we have two systems of inequalities. The lowest population is 250, this means that our value will be greater than or equal to it. While the highest value is 275, this means that our value must be less than or equal to this.

Therefore, the answer is:

A.

`\begin{gathered} P\ge250e^(0.048t) \\ P\leq275e^(0.048t) \end{gathered}`