Question

Ceres has an orbital period of 4.60 years. What is its semimajor axis? Where in the Solar System does this place Ceres?

Answer 1

Given:

The orbital period of the Ceres, T=4.60 years

To find:

The semimajor axis of the orbit of the Ceres.

Step-by-step explanation:

1 year is 3.154×10⁷ s

Thus the orbital period in seconds is given by,

`\begin{gathered} T=4.60*3.154*10^7 \\ =1.451*10^8\text{ s} \end{gathered}`

From Kepler's third law, the orbital period is related to the semi-major axis as,

`T^2=(4\pi^2)/(GM)a^3`

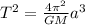
Where G is the gravitational constant, M is the mass of the sun, and a is the semimajor axis.

On substituting the known values,

`\begin{gathered} (1.451*10^8)^2=(4\pi^2)/(6.67*10^(-11)*2*10^(30))* a^3 \\ \Rightarrow a=\sqrt[3]{((1.451*10^8)^2*6.67*10^(-11)*2*10^(30))/(4\pi^2)} \\ =4.14^(11)\text{ m} \end{gathered}`

The semimajor axis of the mars is 2.28×10¹¹ m

The semimajor axis of the Jupiter is 7.78×10¹¹ m

Thus the Ceres is in between the mars and the Jupiter.

Final answer:

The semimajor axis of the Ceres is 4.41×10¹¹ m. Thus it is between Mars and Jupiter.