We are give that at an interval of 51 seconds, 889 hailstones hit a window. To determine the force we need to do a balance of momentum, like this:
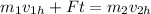
Where:
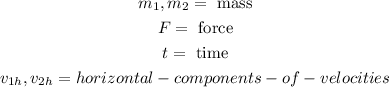
Assuming that the window is completely vertical, then we have:
Therefore, we have that the horizontal component of the velocity when hitting the window is:

And the horizontal component of the velocity after hitting the window is:
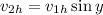
Where the angle "y" is unknown.
Substituting in the balance of momentum we get:
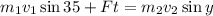
Since the masses are equal for each hailstone, we have:
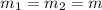
substituting we get:
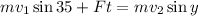
Now, we need to determine the value of the angle after the hailstone hits the window. we are given that the collision is elastic, therefore, we have:
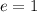
Where "e" is the coefficient of restitution.
The coefficient of restitution is the quotient between the final and initial velocities, therefore, we have:
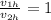
Substituting the values in terms of sines:
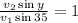
Multiplying both sides by the denominator we get:
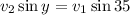
Now, we divide both sides by "sin(y)":
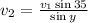
Now, if we consider the balance of momentum in the vertical direction, we have that:
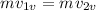
In this case, we don't have a term associated with a force since only the horizontal component of the momentum is associated with the impulse. The verticals components of the velocities are:
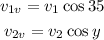
Substituting we get:
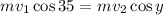
We can cancel out the masses:
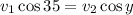
Now, we substitute the value we determine of the second velocity in terms of sines, we get:
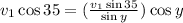
Now, we cancel out the velocity 1:

Now, we divide both sides by sin(35):
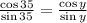
We have that:

Therefore, we have:
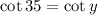
Therefore:
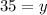
This means that the hailstones have the same angle after they hit the window.
Now, we go back to the equation for the second velocity and substitute the value of "y":
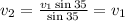
Therefore, the velocities have the same magnitude, but they have opposite directions, therefore.
This means that:
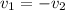
Substituting in the balance of momentum:
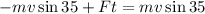
We have taken the velocities in the direction of the window as negative and the direction leaving the window as positive
Now, we solve for the force "F":
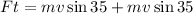
Adding like terms:
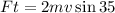
Now, we divide both sides by "t":
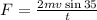
This is the force for one single hailstone, to determine the total force we need to multiply the mass by the 889 hailstones, therefore:
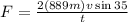
Now, we plug in the values:

Solving the operations:
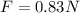
Therefore, the average force on the window is 0.83 Newtons.
Part B. We are asked to determine the pressure on the window. To do that we will use the following formula:

Where:
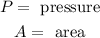
Now, we plug in the values:
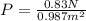
Solving the operations:
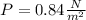
Therefore, the pressure is 0.84 N/m^2