Question

For f(x)=3x and g(x)=x+1(g o f)(x) =?

Answer 1

We have two function

`f(x)=3x`

and

`g(x)=x+1`

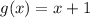
We need to find the composition of these function, i.e.

`(g\circ f)(x)`

Now, notice the following diagram

then, we have defined the composition via our diagram, i.e.

`(g\circ f)(x)=g(f(x))`

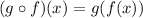
We need to find first the image of x via f, and then to this image f(x), find the image via g, as follows