Question

A baseball is thrown vertically upward at a rate of 80 feet per second from an initial height of 3 feet. Look at photo that I added

Answer 1

The given information is:

The baseball is thrown at a rate of 80 ft/s (this is the initial velocity v0).

The initial height of the baseball is 3 ft (This is the initial height h0).

The projectile formula is:

`h=-16t^2+v_0t+h_0`

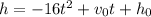
We need to determine when the height of the ball will be 70 feet.

Then replace h=70, v0=80 and h0=3, and solve for t as follows:

`\begin{gathered} 70=-16t^2+80t+3 \\ Subtract\text{ 70 from both sides} \\ 70-70=-16t^2+80t+3-70 \\ 0=-16t^2+80t-67 \end{gathered}`

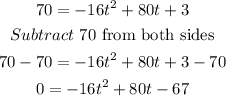
Now we have a quadratic equation in the form 0=at^2+bt+c. Where a=-16, b=80 and c=-67.

We can apply the quadratic formula to solve for t:

`\begin{gathered} t=(-b\pm√(b^2-4ac))/(2a) \\ t=(-80\pm√(80^2-4(-16)(-67)))/(2(-16)) \\ t=(-80\pm√(6400-4288))/(-32) \\ t=(-80\pm√(2112))/(-32) \\ t=(-80\pm45.96)/(-32) \\ t=(-80+45.96)/(-32)=1.06\text{ and }t=(-80-45.96)/(-32)=3.94 \end{gathered}`

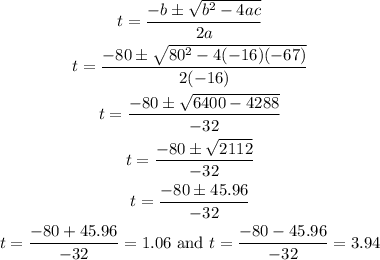
Thus, the baseball is at 70 feet after 1.06,3.94 seconds.