Question

Suppose that the function f is defined on the interval (-2, 2) as follows.-2 if – 2

Answer 1

Given the function f which is defined as follows:

`f(x)=\begin{cases}-2,-2\le x<-1 \\ -1,-1\le x<0 \\ 0,0\le x<1 \\ 1,1\le x<2 \\ \end{cases}`

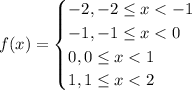
To find the value of the function at a certain point of x, the value of x must satisfy the corresponding inequality

To find f(-2):

-2 lies in the first interval, f(-2) = -2

f(-0.5)

x = - 0.5 lies in the second interval, f(-0.5) = -1

f(1)

x = 1 lies in the fourth interval , f(1) = 1