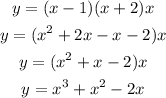Question

Determine the equation of a cubic function passing through +1 and touching -2.

Answer 1

Let's assume +1 and -2 refers to the ordered pairs (1, 0) and (-2, 0).

That means the cubic function has the x-intercepts at (1, 0) and (-2, 0), therefore x = 1 and x = -2 are two of the zeros of the function.

The factored form of a cubic equation is given by:

`y=a(x-x_1)(x-x_2)(x-x_3)`

Where x1, x2 and x3 are the zeros of the function.

We have x1 = 1 and x2 = -2, so let's choose x3 = 0 and a = 1, then we have the following equation:

`\begin{gathered} y=(x-1)(x+2)x \\ y=(x^2+2x-x-2)x \\ y=(x^2+x-2)x \\ y=x^3+x^2-2x \end{gathered}`