1 Answer

Richard Schwartz · Answer 1 · 2023-12-25T21:11:03+0000

Given that the mass of the ball, m = 5 kg

The initial velocity of the ball is

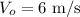
$V_o=6\text{ m/s}$

The final velocity of the ball is

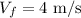
$V_f=4\text{ m/s}$

We have to find the work done.

The work done can be calculated by the formula,

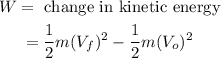
$\begin{gathered} W=\text{ change in kinetic energy} \\ =(1)/(2)m(V_f)^2-(1)/(2)m(V_o)^2 \end{gathered}$

Substituting the values, the work done will be

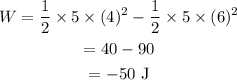
$\begin{gathered} W=(1)/(2)*5*(4)^2-(1)/(2)*5*(6)^2 \\ =40-90 \\ =-50\text{ J} \end{gathered}$

Thus, the work done will be -50 J

Please log in or register to add a comment.