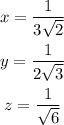Given:
The right triangles are given.
To find: The value of x, y, and z
Step-by-step explanation:
We know that,
The altitude drawn to the hypotenuse of a right triangle creates two similar right triangles, each similar to the original right triangle and similar to each other.
Furthermore, the triangles are similar to each other by AA similarity.
From the small two right triangles,
We can write it as,
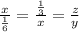
Solving the first two terms,
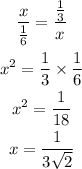
Then using the Pythagoras theorem,
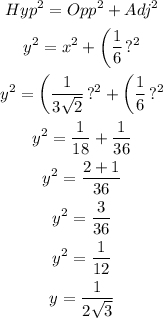
Again using the Pythagoras theorem,
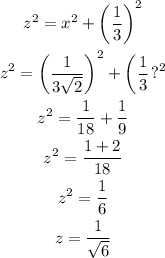
Final answer: The values are,