Given the following function:

Use the form a·cot(bx - c) to find the variables used to find the amplitude, period, phase shift and vertical shift.
We get,
a = 1
b = 1
c = -π/6
d = 0
Since the graph of the Cotangent function does not have a maximum or minimum value, there can be no value for the amplitude.
Amplitude: None
For the Period:
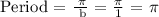
Therefore, the Period is π.
For the Phase Shift:
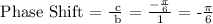
Therefore, Phase Shift is -π/6 → π/6 (To the left).
For the Vertical Shift:
Vertical Shift = 0
Plotting the function will be: