Step-by-step explanation
Given
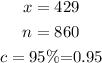
We can fid
Part A: Construct a 95% confidence interval
The best point estimate of the population proportion p is the sample proportion. The sample proportion is the number of successes divided by the sample size
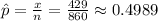

Therefore, we can calculate the margin of error as

The boundaries of the confidence interval are then
Answer
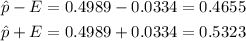
Part B:
We are 95% confident that the true proportion of boys in all births is between 0.4655 and 0.5323
By observation, we can see that 0.512 is between 0.4655 and 0.5323, thus these sample results do not provide strong evidence against the belief that the proportion is 0.512.
Answer: No