Question

10) A rectangular strip of aluminum, 30 cm long and 10 cm wide, is rolled into the form of a cylinder.Which would have the greater volume, a cylinder 10 cm high with circumference of 30 cm or a cylinder30 cm high with circumference of 10 cm? Show the math that leads you to this conclusion.

Answer 1

We have the following cases:

1. A cylinder 10 cm high with a circumference of 30 cm.

2. A cylinder 30 cm high with a circumference of 10 cm.

The circumference is equal to 2 * pi * r.

Then, we can see that, for the first case, we have:

Then, the radius for this case is:

`r_1=(30)/(2\cdot\pi)`

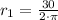
The radius for the second case is:

The radius is:

`r_2=(10)/(2\cdot\pi)`

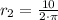
Then, we need to use the formula to find the volume of a cylinder.

First Case:

`V_1=\pi\cdot r^2\cdot h\Rightarrow V_1=\pi\cdot((30)/(2\pi))^2\cdot10=716.1972`

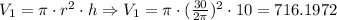
Second Case:

`V_2=\pi\cdot((10)/(2\cdot\pi))^2\cdot30=238.7324`

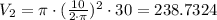
Therefore, according to the results, V1 > V2 (716.1972 cm^3 > 238.7324 cm^3), that is, a cylinder 10cm high with a circumference of 30cm has a greater volume than a cylinder 30 high with a circumference of 10 cm.