Question

You roll a number cube and flip a coin. Which probability does not belong with The other three

Answer 1

Given:

We roll a number cube and flip a coin.

The sample space is

`S=\mleft\lbrace(1,T),(2,T),(3,T),(4,T),(5,T),(6,T),(1,H),(2,H),(3,H),(4,H),(5,H),(6,TH)\mright\rbrace`
`n(S)=12`

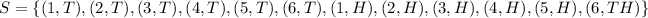
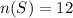
1)

Let A be the event getting the number less than 2 and heads.

`A=\lbrack(1,H)\}`
`n(A)=1`

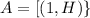
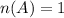
The probability is

`P(A)=(n(A))/(n(S))=(1)/(12)`

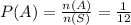
2)

Let B be the event getting the number less than 2 and tails.

`B=\lbrack(1,T)\}`
`n(B)=1`

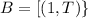
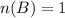
The probability is

`P(B)=(n(B))/(n(S))=(1)/(12)`

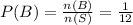
3)

Let C be the event getting the number greater than 2 and tails.

`C=\mleft\lbrace(3,T),(4,T),(5,T),(6,T)\mright\rbrace`
`n(C)=4`

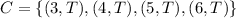
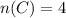
The probability is

`P(C)=(n(C))/(n(S))=(4)/(12)=(1)/(3)`

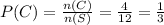
4)

Let D be the event getting the number greater than 5 and heads.

`D=\mleft\lbrace(6,H\mright)\}`

`n(D)=1`

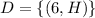
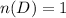
The probability is

`P(D)=(n(D))/(n(S))=(1)/(12)`

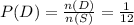
Hence we get

P(less than 2 and tails)=1/12

P(less than 2 and heads)=1/12

P(greater than 2 and tails)=1/3

P(greater than 5 and heads)=1/12

P(greater than 2 and tails) is not belonging to others.