Answer:
x > - 5
Step-by-step explanation:
The initial expression is:
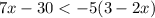
First, we can apply distributive property on the right side as follows:
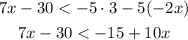
Now, we can add 30 to both sides:
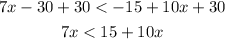
Subtracting 10x from both sides:
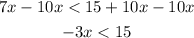
Finally, we need to divide by -3 but since -3 is a negative number, we change the symbol of the inequality as:
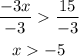
Therefore, the solution is x > - 5