Solution
- We are asked to find the number of times the two cosine graphs intersect:
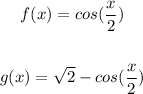
- We have also been restricted to the domain of [0, 360). This implies that we are considering all the angles from 0 (Inclusive) to 360 (not included).
- The point where both f(x) and g(x) intersect, implies that they are equal at that point. Thus, we can simply equate both functions together and solve for x to get all the values of x within the domain [0, 360).
- This is done below:
![\begin{gathered} f(x)=cos((x)/(2)) \\ \\ g(x)=√(2)-cos((x)/(2)) \\ \\ Equate\text{ the equations,} \\ f(x)=g(x) \\ That\text{ is,} \\ \\ cos((x)/(2))=√(2)-cos((x)/(2)) \\ Add\text{ }cos((x)/(2))\text{ to both sides} \\ \\ cos((x)/(2))+cos((x)/(2))=√(2) \\ \\ 2cos((x)/(2))=√(2) \\ \\ Divide\text{ both sides by 2} \\ \\ cos((x)/(2))=(√(2))/(2) \\ \\ Take\text{ the inverse cosine of both sides} \\ (x)/(2)=cos^(-1)((√(2))/(2)) \\ \\ \text{ Using the reference angles, we know that} \\ 45\degree,315\degree,...=cos^(-1)((√(2))/(2)) \\ \\ Thus,\text{ we can say} \\ (x)/(2)=45\degree,315\degree,... \\ \\ Multiply\text{ both sides by 2} \\ \\ x=2(45\degree),2(315\degree),... \\ x=90\degree,630\degree,... \\ \\ But\text{ we have been told that the domain of the solution must lie within \lbrack0, 360\rparen} \\ \\ This\text{ means we discard all values after 90 degrees.} \\ \\ \therefore x=90\degree \end{gathered}]()
Final Answer
The answer is 90° (OPTION 1)