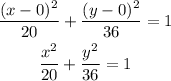Question

Find the standard form of the equation for the ellipse with foci (0,+-4) and vertex (0,6)

Answer 1

Since the x-coordinates are equal, the ellipse is vertical. Thus, the standard equation of the ellipse is as follows:

`((x-h)^2)/(b^2)+((y-k)^2)/(a^2)=1`

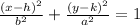
Since the x-coordinates of the foci and the vertex are the same, the value of h must be 0.

Equate the y-coordinates of the foci to the following.

`\begin{gathered} k+c=4 \\ k-c=-4 \end{gathered}`

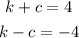
Add the two equations and then solve for k.

`\begin{gathered} 2k=0 \\ k=0 \end{gathered}`

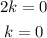
Thus, the center is at (0,0) or the origin.

To solve for c, substitute the value of k into k+c=4.

`\begin{gathered} k+c=4 \\ 0+c=4 \\ c=4 \end{gathered}`

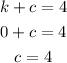
To solve for a, equate the y-coordinate of the vertex to k+a.

`\begin{gathered} k+a=6 \\ 0+a=6 \\ a=6 \end{gathered}`

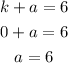
Solve for a².

`a^2=6^2=36`

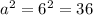
To solve for b², substitute the value of a and c into the following equation.

`b^2=a^2-c^2`

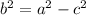
Thus, we obtain the following:

`\begin{gathered} b^2=6^2-4^2 \\ b^2=36-16 \\ b^2=20 \end{gathered}`

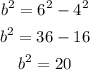
Substitute the values into the equation of the ellipse. Thus, we obtain the following:

`\begin{gathered} ((x-0)^2)/(20)+\frac{(y-0)^2}{36^{}}=1 \\ (x^2)/(20)+\frac{y^2}{36^{}}=1 \end{gathered}`