1 Answer

Unforgiven · Answer 1 · 2023-01-16T09:58:24+0000

We are asked to simplify the following expression:

$\sqrt[]{125}\cdot(\sqrt[]{5}-\sqrt[]{7})$

We can begin with solving the square root of 125.

125 can be expressed as:

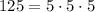
$125=5\cdot5\cdot5$

5 cubed is equal to 125.

Since we have a square root, it is convenient to express that 125 in squares:

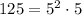
$125=5^2\cdot5$

Then, for the square root of 125:

$\sqrt[]{125}=\sqrt[]{5^2\cdot5}$

The square root of a product is equivalent to the product of the square roots:

$\sqrt[]{125}=\sqrt[]{5^2}\cdot\sqrt[]{5}$

We know that the square root of 5 squared is 5:

$\sqrt[]{5^2}=5$

Then, we can say that:

$\sqrt[]{125}=5\cdot\sqrt[]{5}$

We can replace the term in the first equation:

$\sqrt[]{125}\cdot(\sqrt[]{5}-\sqrt[]{7})=5\cdot\sqrt[]{5}\cdot(\sqrt[]{5}-\sqrt[]{7})$

Now, we can solve the parenthesis:

$5\cdot\sqrt[]{5}\cdot(\sqrt[]{5}-\sqrt[]{7})=5\cdot\sqrt[]{5}\cdot\sqrt[]{5}-5\cdot\sqrt[]{5}\cdot\sqrt[]{7}$

The product of the square roots is equivalent to the square root of the product, then:

$\begin{gathered} 5\cdot\sqrt[]{5\cdot5}-5\cdot\sqrt[]{5\cdot7} \\ 5\cdot\sqrt[]{25}-5\cdot\sqrt[]{35} \\ 5\cdot5-5\cdot\sqrt[]{35} \end{gathered}$

Finally, the expression simplified will be:

$25-5\cdot\sqrt[]{35}$

Please log in or register to add a comment.