Question

Sea f(x) = 2x3 – 3x2 – 12x + 1 a) Halle los valores críticos de f(x) usando primera derivada, luego evalúe en f(x) y señale el máximo y el mínimo.

Answer 1

Tenemos la siguiente funcion:

`f(x)=2x^3-3x^2-12x+1`

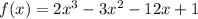
La primera derivada nos da

`f^(\prime)(x)=2\cdot(3x^2)-3\cdot(2x)-12`

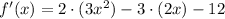
donde hemos usado la regla de derivacion:

`x^n\Rightarrow nx^(n-1)`

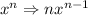
Igualando a cero para obtener los puntos criticos tenemos:

`\begin{gathered} f^(\prime)(x)=2\cdot(3x^2)-3\cdot(2x)-12=0 \\ \text{esto es} \\ 6x^2-6x-12=0 \end{gathered}`

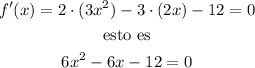
Si factorizamos un 6, podemos reescribir lo anterior como

`\begin{gathered} 6(x^2-x-2)=0 \\ lo\text{ cual implica que},\text{ la expresion anterior se reduce a} \\ x^2-x-2=0 \end{gathered}`

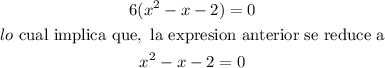
Entonces, para obtener x, debemos usar la solucion general de segundo grado:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{que viene del la ecuacion cuadratica:} \\ ax^2+bx+c=0 \end{gathered}`

Como vemos, en nuestro caso, a=1, b=-1 y c=-2. Sustituyendo estos valores en la formula anterior, tenemos

`x=\frac{-(-1)\pm\sqrt[]{(-1)^2-4(1)(-2)}}{2(1)}`

lo cual nos da:

`\begin{gathered} x=\frac{1\pm\sqrt[]{1+8}}{2} \\ es\text{ decir} \\ x=\frac{1\pm\sqrt[]{9}}{2} \\ x=(1\pm3)/(2) \end{gathered}`

Tenemos entonces dos soluciones, cuando el signo de enmedio es + y cuando es -. Es decir,

`\begin{gathered} x_1=(1+3)/(2)=(4)/(2)=2 \\ y \\ x_2=(1-3)/(2)=-(2)/(2)=-1 \end{gathered}`

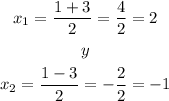
Por tanto, los valores criticos ocurren cuando x=2 y cuando x= -1. Tenemos entonces que,

a) Halle los valores críticos de f(x) usando primera derivada:

Cuando x=2, tenemos en nuestra funcion original que

`f(2)=2(2)^3-3(2)^2-12(2)+1`

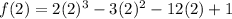
lo cual da

`\begin{gathered} f(2)=16-12-24+1 \\ f(2)=17-36 \\ f(2)=-19 \end{gathered}`

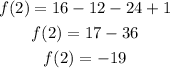
Ahora, cuando x=-1, tenemos

`\begin{gathered} f(-1)=2(-1)^3-3(-1)^2-12(-1)+1 \\ f(-1)=-2-3+12+1 \\ f(-1)=13-5 \\ f(-1)=7 \end{gathered}`

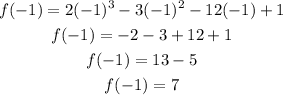
es decir, los puntos criticos son (2,-19) y (-1,7).

a2) luego señale el máximo y el mínimo.​

El criterio para saber si un punto es maximo o minimo es el siguiente:

`\begin{gathered} Si\text{ f''(x)<0 tenemos un MAXIMO} \\ Si\text{ f''(x) >0 tenemos un MINIMO} \end{gathered}`

La segunda derivada de nuestra funcion es:

`f^{\prime^(\doubleprime)}(x)=2\cdot3\cdot2x-3\cdot2`

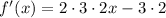
la cual da

`f´´(x)=12x-6`

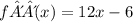
Entonces, en nuestro primer punto critico, cuando x=2, tenemos que

`\begin{gathered} f´´(2)=12(2)-6 \\ f´´(2)=24-6=18 \end{gathered}`

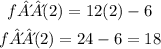
que es mayor a cero. Por tanto, en el punto (2,-19) tenemos un MINIMO.

De forma similar, para el segundo punto critico, sustituyendo x=-1 en nuestra segunda derivada tenemos:

`f´´(-1)=12(-1)-6=-12-6=-18`

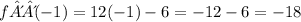
que es menor que cero. Por tanto, en el punto (-1, 7) tenemos un MAXIMO