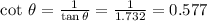Question

Find the value of each of the six trigonometric functions of the angle 0 in the figure.

Answer 1

We first need to calculate the missing side of the triangle. We can do that by applying Pithagora's theorem as shown below:

`\begin{gathered} 20^2=10^2+x^2 \\ x^2=400-100 \\ x^2=300 \\ x=17.32 \end{gathered}`

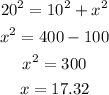
We can now calculate the trigonometric figures. We will start by the sine.

`\begin{gathered} \sin \theta=\frac{oposite\text{ side to the angle }\theta}{\text{hypothenuse}}=(17.32)/(20)=0.866 \\ \end{gathered}`

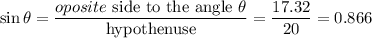
We can then calculate the cosecant:

`\text{ cossec }\theta=(1)/(\sin \theta)=(1)/(0.866)=1.155`

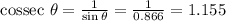
We will then calculate the cosine.

`\cos \theta=\frac{\text{ adjacent side to the angle }\theta}{\text{hypothenuse}}=(10)/(20)=0.5`

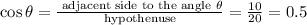
We can calculate the secant:

`\sec \theta=(1)/(\cos \theta)=(1)/(0.5)=2`

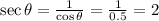
We will then calculate the tangent:

`\tan \theta=\frac{\text{ opposite side to the angle }\theta}{\text{ adjacent side to the angle }\theta}=(17.32)/(10)=1.732`

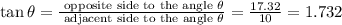
We can now calculate the cotangent:

`\text{ cot }\theta=(1)/(\tan \theta)=(1)/(1.732)=0.577`