Question

F(x) = x² over the interval [1,∞)
This is one-to-one

Answer 1

Part a

we have the function

`\begin{gathered} f(x)=x^4 \\ interval\text{ \lbrack1,}infinite) \end{gathered}`

Remember that

A function is one-to-one if every element of the range corresponds to exactly one element of the domain

using a graphing tool

The answer Part a is

This is one-to-one

Part B

we have the function

`f(x)=(e^x)^2`

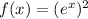
interval -----> All real numbers

using a graphing tool

The answer Part B is

This is one to one

Part C

we have the function

`f(x)=(\log_2x)^2`

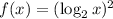
Interval ----> All real numbers

The answer Part C is

Is not one to one function

Part D

we have the function

`f(x)=(x-2)^4`

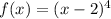
interval [0,infinite)

using a graphing tool

The answer Part D is

Is not one to one function

Part E

we have the function

`f(x)=\sqrt[3]{x}`

Interval ----> all real numbers

using a graphing tool

The answer Part E is

Is one to one function