ANSWER:
(a)
B.
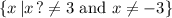
(b)
A.
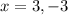
(c)
A.

(d)
Explanation:
We have the following function:
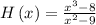
(a)
The domain is the input values of the function that get an output value. In this case they are all the values that x can take while the function is still defined.
In a fractional function, the only way for it to be indefinite is for the denominator to be 0.
Therefore, we set it equal to 0, just like this:
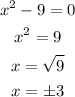
Therefore, the domain would be all real numbers except 3 and -3.
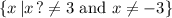
(b)
The vertical asymptotes are the values of x when the function is not defined.
They are the same values obtained in the domain, therefore:

(c)
The horizontal asymptote is calculated with the quotient between the terms of higher degree in the numerator and the denominator, therefore:
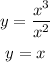
The only graph that complies with the above is graph A: