Question

Fine the x and y intercepts of the following equation. Fill in blank one and blank two.

Answer 1

Step-by-step explanation:

We are given the following linear equation;

`2x+3y=12`

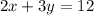
We would begin by re-writing the equation in the slope-intercept form as shown below;

`y=mx+b`

We now have;

`\begin{gathered} 2x+3y=12 \\ Make\text{ y the subject of the equation;} \end{gathered}`
`3y=12-2x`
`\begin{gathered} Divide\text{ all through by 3;} \\ (3y)/(3)=(12)/(3)-(2x)/(3) \end{gathered}`
`y=4-(2)/(3)x`

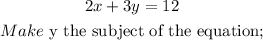
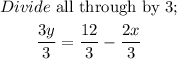
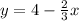
We can re-arrange this in the format shown earlier;

`y=-(2)/(3)x+4`

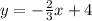
The x-intercept is derived at the point where y = 0. Same for the y-intercept. Its derived at the point where x = 0.

Hence, for the equation;

`\begin{gathered} y=-(2)/(3)x+4 \\ When\text{ }x=0 \\ y=-(2)/(3)(0)+4 \\ y=4 \end{gathered}`
`\begin{gathered} When\text{ }y=0 \\ 0=-(2)/(3)x+4 \\ (2)/(3)x=4 \end{gathered}`

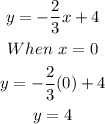
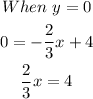
Cross multiply and we'll have;

`\begin{gathered} 2x=3*4 \\ 2x=12 \\ \end{gathered}`

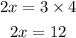
Divide both sides by 2;

`x=6`

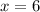
Therefore, the x and y intercepts are;

ANSWER:

`\begin{gathered} x-intercept=6 \\ y-intercept=4 \end{gathered}`