Question

Solve the following system of the equalities by graphing. Graph the system below and enter the solution set as an ordered pair in the form (x,y). If there are no solution, enter none and all if there are no solutions X + 2y = 3 3x + 6y = 15

Answer 1

No solution

1) Since we are about to solve this system graphically, then let's set two t-tables picking random values for x, plugging them into each function to get at least three coordinate pairs (points), and plot them.

2) Considering the 1st equation:

I) x+2y=3

Let's rewrite into the Slope-intercept form:

`\begin{gathered} x+2y=3 \\ 2y=3-x \\ (2y)/(2)=(3)/(2)-(x)/(2) \\ y=-(x)/(2)+(3)/(2) \end{gathered}`

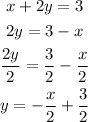
x | y

-1 | 2

0 | 3/2

1 | 1

(-1,2) , (0, 3/2), (1,1) These are the points we are going to use, considering that the slope is negative.

II) 3x+6y=15

Rewriting into the Slope intercept form, for convenience, we can set the following t-table.

`\begin{gathered} 3x+6y=15\: \\ 3x+6y=15(\: /3) \\ x+2y=5 \\ x-x+2y=5-x \\ 2y=5-x \\ (2y)/(2)=(5-x)/(2) \\ y=(5)/(2)-(x)/(2) \end{gathered}`

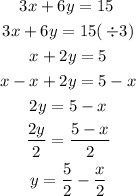
x|y

-1| 3

0| 5/2

1| 2

(-1,3), (0,5/2), (1,2)

3) So let's plot those points considering a decreasing slope for both equations:

his is the graph, as we can see there's no common point to any of those equations (represented by lines). Hence, we can state that There is no solution