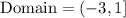THis is the graph of a positive parabola, that opens upward.
The equation is:
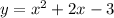
The general form of a quadratic is >>>
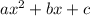
So,
a = 1
b = 2
c = -3
(a)
The vertex is the lowest point of the parabola. The x-coordinate is:
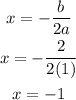
And y is:
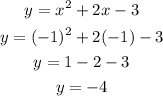
The vertex is at (-1, -4).
(b)
The range is the set of y-values for which a function is defined. From the graph, we can see that the parabola is defined from y = -4 to y = 0. In interval notation >>>
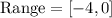
(c)
The domain is the set of x-values for which a function is defined.
The two x-axis points are the x-intercepts. They are found below:
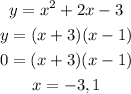
From the graph, we can see that the parabola is defined from x = -3 (not included point) until x = 1. So, the domain is >>>