Question

3) 4) 35-360320 90°-45°-45° 360°+36044 Jet 2130 Draw an angle with the given measure in standard position.

Answer 1

1/12π

9) Considering that the reference angle is an acute angle, (less than 90º or

π/2) then we can write out (in degrees to make it easier to grasp it then in π radians):

`-(47\pi)/(12)=-705^(\square)`

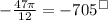
So we can subtract 360º, 705º-360º= 345º. Subtracting once more:

360º-345º = -15º. Writing that in Pi radians we've got:

`\begin{gathered} -(47\pi)/(12)+2\pi=-(23\pi)/(12) \\ -(23\pi)/(12)+2\pi=(1)/(12)\pi \end{gathered}`

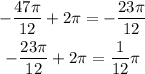
2) Recap:

• Check if the angle is greater than 360º (or 2π) If it is so you can subtract it from 360º(2π)

• As in this case, 345º is in the Quadrant IV, then we'll subtract it again from 360º.

,

• Since the given angle is negative (Counterclockwise) then we add to perform that subtraction again: 360-345 = 15º or 2π -23/12 π = 1/12π

3) Hence, the answer is 1/12π