Question

Please do #1 under where it says “Mixed review slide 8”

Answer 1

The coins are in the shape of a cylinder.

The formula to calculate the volume of a cylinder is given as

`V=\pi r^2h`

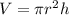
where

`\begin{gathered} r=\text{ radius} \\ h=\text{ height} \end{gathered}`

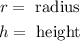
The individual coin has the following dimensions:

`\begin{gathered} r=1\text{ in} \\ h=0.0625\text{ in} \end{gathered}`

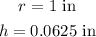
Thus, the volume of one coin can be calculated as

`\begin{gathered} V=\pi*1^2*0.0625 \\ V=0.196\text{ cubic inches} \end{gathered}`

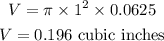
If there are 225 coins in the chest, the combined volume of all the coins will be

`\begin{gathered} V_T=0.196*225 \\ V_T=44.1\text{ cubic inches} \end{gathered}`

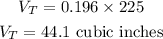
The combined volume is 44.1 cubic inches.