Question

The function f(x) = 2x ^ 3 - 36x ^ 2 + 162x + 8 has one local minimum and one local maximum Use a graph of the function to estimate these local extrema This function has a local minimum at c = with output value

Answer 1

Given:

There are given the function:

`f(x)=2x^3-36x^2+162x+8`

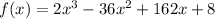
Step-by-step explanation:

According to the question:

We need to find the local minima and local maxima:

So,

To find the derivatives, first, we need to find the derivatives of the given function:

So,

From the function:

`f(x)=2x^(3)-36x^(2)+162x+8`

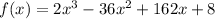
Then,

From the first derivatives:

`\begin{gathered} f(x)=2x^(3)-36x^(2)+162x+8 \\ f^(\prime)(x)=6x^2-72x+162 \end{gathered}`

Then,

Find where the first derivative is equal to 0 to find the local maxima and minima:

So,

`\begin{gathered} f^(\prime)(x)=6x^(2)-72x+162 \\ 0=6x^2-72x+162 \end{gathered}`

Then,

`\begin{gathered} 0=6x^(2)-72x+162 \\ 0=x^2-12x+27 \end{gathered}`

Then,

`\begin{gathered} x^2-12x+27=0 \\ x^2-9x-3x+27=0 \\ (x-9)(x-3)=0 \\ x=9,3 \end{gathered}`

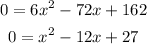
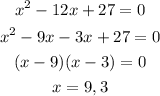
Then,

Put the value of 3 and 9 for x into the given function:

So,

First put 3 for x:

`\begin{gathered} f(x)=2x^(3)-36x^(2)+162x+8 \\ f(3)=2(3)^3-36(3)^2+162(3)+8 \\ f(3)=54-324+486+8 \\ f(3)=224 \end{gathered}`

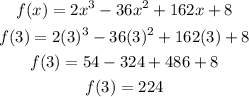
And,

Put 9 for x:

`\begin{gathered} f(x)=2x^(3)-36x^(2)+162x+8 \\ f(9)=2(9)^3-36(9)^2+162(9)+8 \\ f(9)=8 \end{gathered}`

Final answer:

Hence, the function has a local minimum at x = 9 with the output value 8 and a local maximum at x = 3 with the output value 224.