Question

This attached math if can help with this problem thanks

Answer 1

Recall that a function f(x) is an exponential function if it is as follows:

`f(x)=ab^x\text{.}`

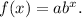
Notice that:

`\begin{gathered} 2=2\cdot1.3^0, \\ 2.6=2\cdot1.3^1, \\ 3.38=2\cdot1.3^2, \\ 4.394=2\cdot1.3^3, \\ 5.7122=2\cdot1.3^4, \\ 7.42586=2\cdot1.3^5\text{.} \end{gathered}`

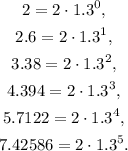
Therefore, the function described by the given table is:

`f(x)=2\cdot1.3^x\text{.}`

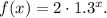
Therefore the given relationship represents an exponential relation.

Answer: The relation between x and y is exponential.