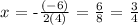Question

Express y = 4x ^ 2 - 6x + 14 in the form y = 4 * (x - p) ^ 2 + q , where p and q are constants. Hence, state the minimum value of y and the value of x at which the minimum value occurs. Find the equation of the line of symmetry.

Answer 1

Step-by-step explanation:

Here, we want to write the given equation in the form stated

We proceed as follows:

`\begin{gathered} y\text{ = 4x}^2-6x\text{ + 14} \\ y\text{ = 4\lparen x-}(3)/(2))\placeholder{⬚}^2+5 \end{gathered}`

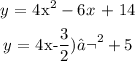
Thus, we have it that p has a value of 3/2 and q has a value of 5

Now, we want to state the minimum value of y and x at which the minimum value occurs

The minimum y value would be the value of q which is 5

The value of x at this y-value is p, which is 3/2

Lastly, we want to find the equation of the line of symmetry

Mathematically, we have that as :

`x\text{ = -}(b)/(2a)`

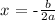
where, b is the coefficient of x which is -6 and a is the coefficient of x^2 which is 4

Thus, we have the equation of the line of symmetry as:

`x\text{ = -}((-6))/(2(4))\text{ = }(6)/(8)\text{ = }(3)/(4)`