Question

Help Soraya decide which tent to buy for her backpacking trip. To make this decision, compare the volumes, floor areas, and surface areas of both tents.

Answer 1

We want to calculate the floor area, surface area, and volume for both tents. Tent A calculations are going to be very easy and we can do it with the values provided, Tent B will be a little bit of a challenge. Because of this, we're starting calculating all the parameters for Tent A.

The floor area is the area of the base. The base of Tent A is a square, and the area of a square is the product of its side length by itself.

`A_f=6^2=36`

The floor area of Tent A is 36 ft².

The first tent has 4 sides and the floor. The "opposite" sides are equal. We have two rectangles with the same measures and two triangles with the same measures. The surface area will be the sum of the area of those sides. The area of a triangle is given by half the product between the height and the base length.

`A_t=(5*6)/(2)=(30)/(2)=15`

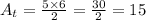
To calculate the area of the rectangular sides we need to calculate the missing side

To find the blue side, we're going to use the Pythagorean Theorem. Let's call its length as x.

`\begin{gathered} 3^2+5^2=x^2 \\ 9+25=x^2 \\ x=√(34) \end{gathered}`

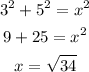
Then, the area of the rectangles is

`A_r=√(34)*6=6√(34)`

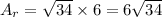
Then, the surface area of the first tent will be the area of the sides plus the floor area.

`\begin{gathered} A_s=2A_t+2A_r+A_f=2*15+2*6√(34)+36 \\ A_s=66+12√(34) \end{gathered}`

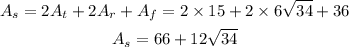
And finally, the volume of the tent will be the triangle side area times the length of the tent.

`A_v=15*6=90`

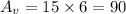
The volume of the tent is 90 ft³.

For the tent B, we have to calculate the slant height before calculating the volume and surface area, so let's do that. In a hexagon, the triangles made by connecting two adjacent vertices to the center are equilateral triangles.

Therefore, we have the following measures in the base of our tent:

Both red segments measure 4', and we can use the pythagorean theorem to calculate the green segment. Let's call it y.

`\begin{gathered} 2^2+y^2=4^2 \\ y^2=16-4 \\ y=2√(3) \end{gathered}`

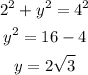
Then, to calculate the slant height, now that we know the measure of the green segment, we can use the pythagorean theorem again. Let's call the slant height as h.

`\begin{gathered} y^2+6^2=h^2 \\ 12+36=h^2 \\ h=√(48)=4√(3) \end{gathered}`

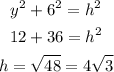
Then, we calculate the missing information. The floor area is the area of the hexagon. The area of the hexagon is given by the following formula

`A_h=(3√(3))/(2)s^2`

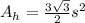
where s represents the side length. The floor area of Tent B is:

`B_f=(3√(3))/(2)(4)^2=24√(3)`

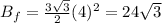
Tent B has 6 equal sides. To calculate the surface area we just have to calculate the area of one side and then multiply it by 6 and add the floor area. We already know how to calculate the area of a triangle, therefore, the surface area of Tent B is

`B_s=6*(4√(3)*4)/(2)+24√(3)=72√(3)`

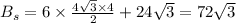
And finally, the volume is given by the following formula

`V=(√(3))/(2)a^2h`

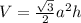
Where h represents the height of the pyramid and a represents the slant height.

The volume of tent B is

`B_v=(√(3))/(2)(4√(3))^2(6)=36√(3)`

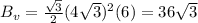
Comparing the floor area, surface area and volume of the tents, we have

[tex]\begin{gathered} B_f>A_f \\ B_s>A_s \\ B_v